Learning Dictionaries with Bounded Self-Coherence
Christian D. Sigg, Member, IEEE, Tomas Dikk and Joachim M. Buhmann, Senior Member, IEEE
This page provides complementary material for our paper on learning dictionaries with bounded self-coherence, published in the IEEE Signal Processing Letters, vol. 19, no. 12, 2012.
Results
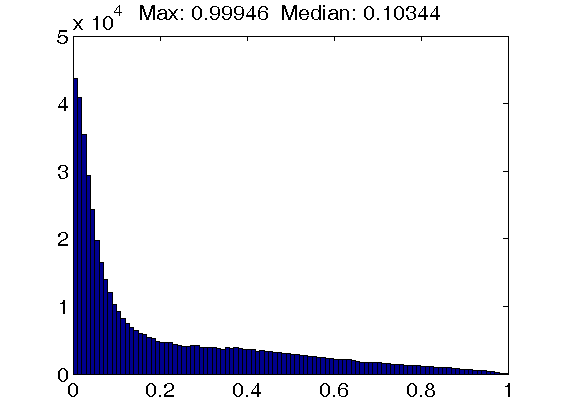
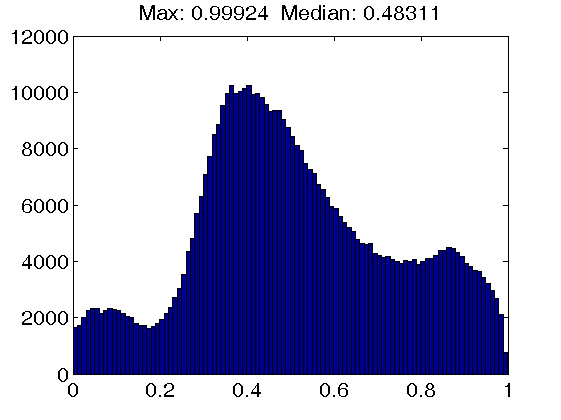
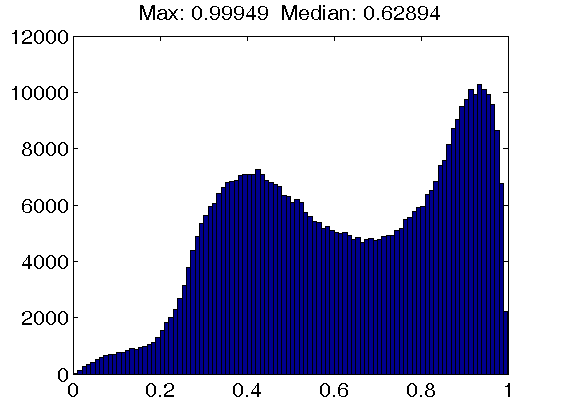
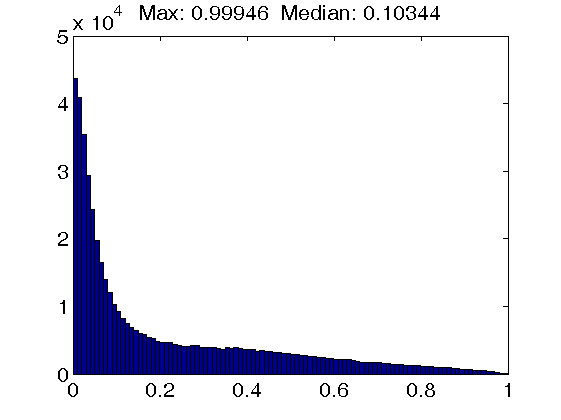
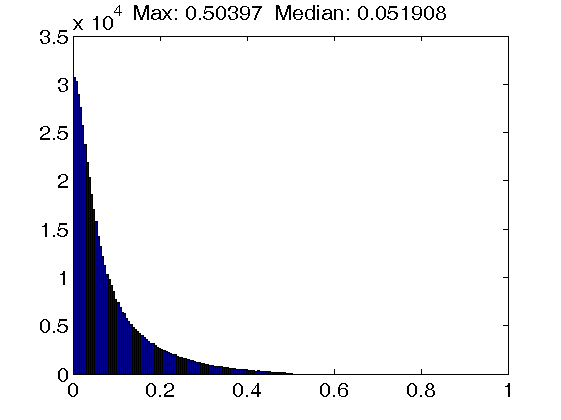
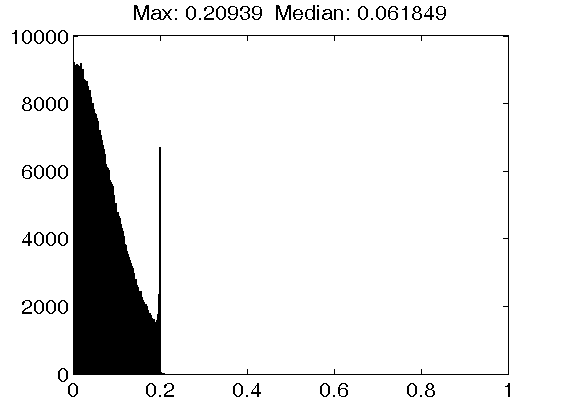
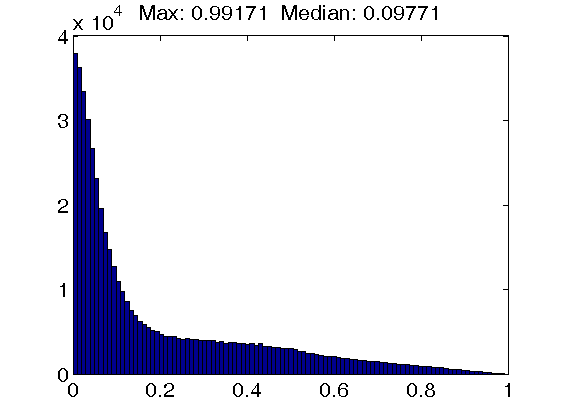
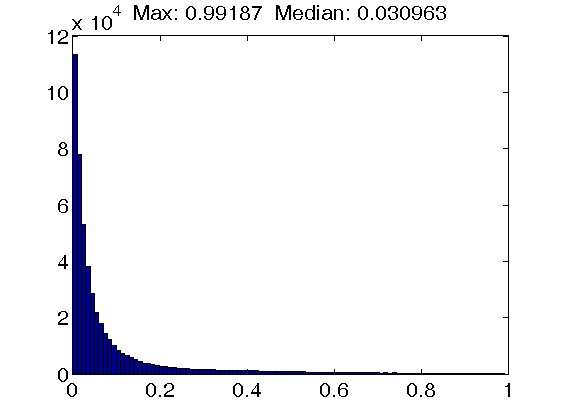
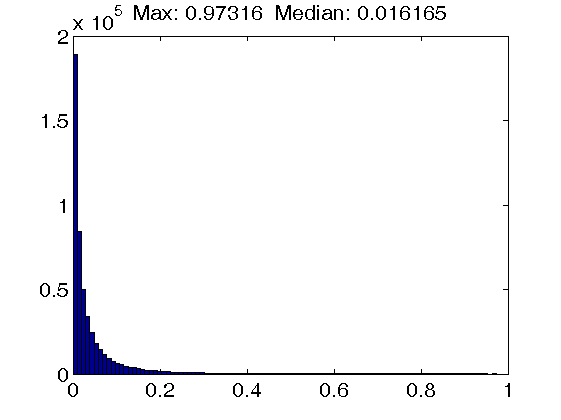
Figure 1. Histograms of atom coherence values. Top row: Results for dictionaries trained with the K-SVD algorithm, using an atom coherence threshold of 1.0 (left figure), 0.5 (middle figure) and 0.2 (right figure). Note that a threshold of 1.0 implies that no atom thresholding takes place. Also, the dictionary self-coherence is actually increasing instead of decreasing when enforcing a tighter threshold.
Middle row: Results for dictionaries trained with the INK-SVD algorithm, using an atom cohrence threshold of 1.0 (left figure), 0.5 (middle figure) and 0.2 (right figure). Note that due to the design of the atom decorrelation step of the INK-SVD algorithm, the maximum coherence value corresponds closely to the atom coherence threshold. Furthermore, note that the median atom coherence value is also increasing instead of decreasing from the middle to the right figure.
Bottom row: Results for dictionaries trained with the IDL(gamma) algorithm, using a penalty of 0 (left figure), 5 (middle figure) and 50 (right figure). Note that while the maximum coherence value is essentially unaffected by the increasing self-coherence penalty, the mass of the distribution concentrates at values close to zero.
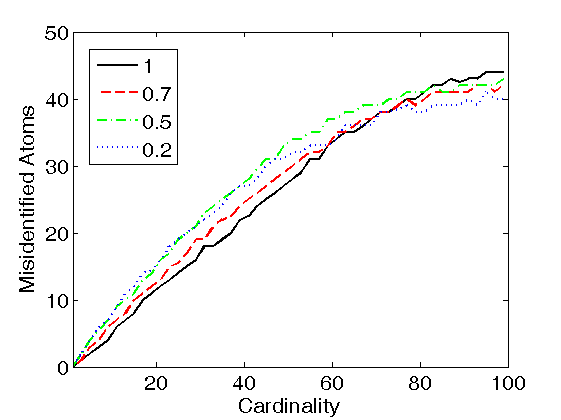
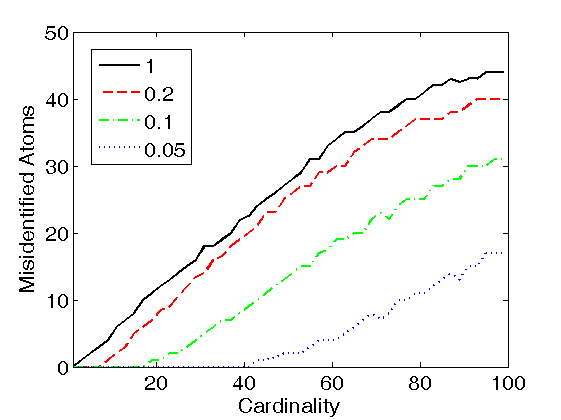
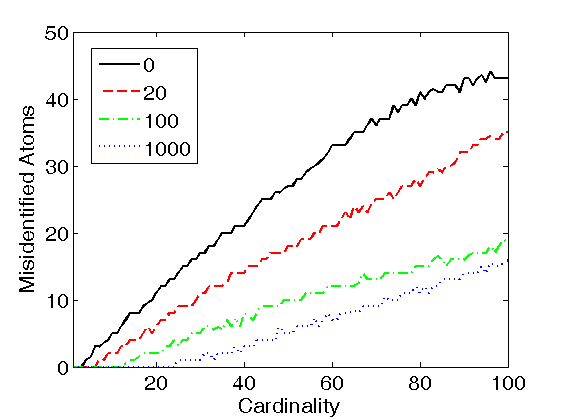
Figure 2. Support recovery with LARC coding in the trained dictionary, as a function of the self-coherence penalty. The coding support of each observation was generated by uniform sampling of K atoms from the trained dictionary (where K is the cardinality of the code, and the dictionary size was set to L=200), and the non-zero coefficients of the code were Gaussian distributed with zero mean and unit variance. The true cardinality K was supplied as the LARC stopping criterion. The number of misidentified atoms was computed by counting all atoms of the true coding support which were not present in the estimated support. Results are shown for dictionaries trained with the K-SVD algorithm (left figure), INK-SVD algorithm (middle figure) and IDL(gamma) algorithm (right figure).