Learning
Bits

Version 0.4 of the nsprcomp package brings several improvements:

• The various deflation methods have been replaced with generalized deflation (Mackey, 2009), which directly optimizes the additional variance explained by each component. Implementing generalized deflation required changes to the inner EM loop, and I was unsure at first whether they could be made efficient for high dimensional data. Fortunately, there is only a small constant increase in computational complexity.

• nscumcomp includes a variational re-normalization step (i.e. recomputing the loadings given the support of the pseudo-rotation matrix), which improves the explained variance quite a bit.

• Both nsprcomp and nscumcomp return the additional explained standard deviation of each component. This is identical to standard PCA for an orthogonal rotation matrix, but avoids double counting of explained variance for principal axes which are not pairwise orthogonal. See the asdev function documentation for details.

A comparison on the marty data from the EMA package illustrates the relative performance of sparse PCA methods with R implementations. This data matrix contains \(N=23\) expression profiles for \(D=54613\) genes, and thus explores the \(N \ll D\) case. The three methods considered are nsprcomp and nscumcomp, and arrayspc from the elasticnet package (version 1.1). PCAgrid from the pcaPP package has problems with long vectors in version 1.9-49 under R 3.0.1 and therefore could not be included in this comparison.

Sequential PCA

arrayspc expects a penalty associated with the \(L_1\) norm of the principal axis as the sparsity argument para (where large penalties lead to sparse solutions). I therefore first ran arrayspc with a constant penalty for all components, measured the cardinalities of the resulting principal axes and used those as the sparsity argument k for nsprcomp.

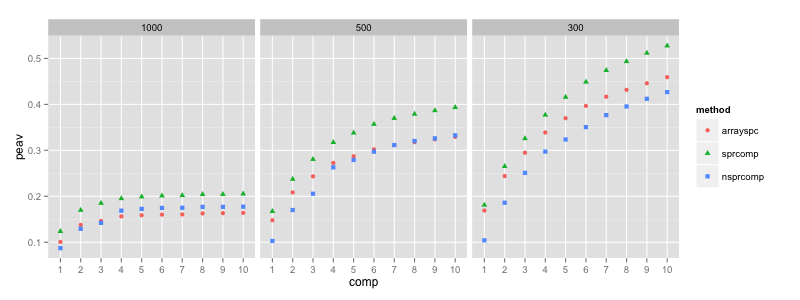
The figure plots the cumulative percentage explained additional variance (see ?peav) w.r.t. the number of components, for an \(L_1\) norm penalty of 1000, 500 and 300, respectively. The number of components was set to 10 in all experiments. “sprcomp” (green triangle) is the result for sparse PCA using nsprcomp, and “nsprcomp” (blue square) is the result for non-negative sparse PCA using nsprcomp. para = 1000 results in cardinalities between 1 and 2823, for para = 300 the cardinalities range between 1716 and 15328. As expected, enforcing additional non-negativity of the loadings resulted in less explained variance.

Cumulative PCA

The comparison of sequential and cumulative methods follows along similar lines. I specified the total sum of all cardinalities as the sparsity argument k to nscumcomp, measured the cardinalities of the resulting principal axes and used those as the sparsity argument for nsprcomp. The number of components was again set to ncomp = 10.

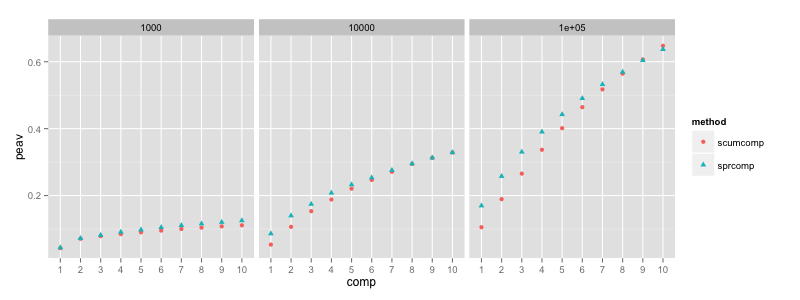
The greedy optimization of nsprcomp (denoted “sprcomp” for sparse PCA) achieves more explained variance for the first components, but its curve also saturates more quickly for the latter components. The nscumcomp curve is more linear, and the total explained variance of both methods is therefore comparable.

Including the non-negativity constraint gives similar results:

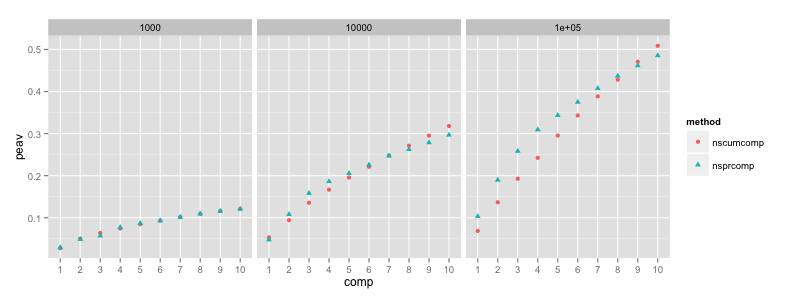
The difference between greedy and joint optimization of the principal axes is most pronounced for k = 1e5. Here, the “nsprcomp” curve saturates so quickly that the almost linear “nscumcomp” curve achieves more explained total variance (this effect would be even greater if ncomp was increased beyond ten). As expected, the additional non-negativity constraint results in less cumulative explained variance overall.

Conclusion

The comparison demonstrates that both nsprcomp and nscumcomp can be used fruitfully to analyze high dimensional data such as gene expression profiles. The explained variance depends on the choice of the constraints and the goal (sequential versus joint analysis), but is comparable between both algorithms and competitive with respect to arrayspc.

References

L. W. Mackey (2009). Deflation Methods for Sparse PCA. Advances in Neural Information Processing Systems, Vol. 21.